|
Camargue
|
|
Camargue
|
Classes and functions related to cut separation. More...
Classes | |
| class | CandidateTeeth |
| class | CCsepBase |
| Abstract base class for calling Concorde separation routines. More... | |
| class | Clique |
| Class for storing segment lists representing edges of a hypergraph. More... | |
| class | CliqueBank |
| Storage of a repository of Cliques, for use in building a HyperGraph. More... | |
| class | ConcordeSeparator |
| Class template for straightforward Concorde separation routines. More... | |
| class | CutQueue |
| Class template for queue of cuts in some form. More... | |
| struct | dominoparity |
| Structure for storing simple DP inequalities. More... | |
| class | DPwitness |
| Class for building miniature simple DP witness cutgraphs. More... | |
| struct | ex_blossom |
| Structure for storing blossom inequalities from exact primal separation. More... | |
| class | ExBlossoms |
| Exact primal blossom separation as per Letchford and Lodi's algorithm. More... | |
| class | ExternalCuts |
| The external storage of a collection of HyperGraph cuts in a Relaxation. More... | |
| class | HyperGraph |
| External representation of a cut added to the lp relaxation. More... | |
| class | LocalCuts |
| Primal separation of non-template local cuts via standard heuristics. More... | |
| class | LPcutList |
| Management of Concorde lpcut_in linked list. More... | |
| class | MetaCuts |
| Separation of cut metamorphoses. More... | |
| struct | MIRgroup |
| Memory-managed access to classes needed during safe GMI separation. More... | |
| class | PoolCuts |
| Cut pool separation. More... | |
| class | SafeGomory |
| Primal separation of safe Gomory cuts. More... | |
| class | Separator |
| Management of basic separation routines. More... | |
| class | SimpleDP |
| Separating primal simple domino parity inequalities. More... | |
| struct | SimpleTooth |
| Representing simple tooth inequalities. More... | |
| struct | SystemDeleter |
| Deleter for constraint matrix system. More... | |
| class | Tooth |
| Vertex set structure used in tooth inequalities for domino parity cuts. More... | |
| class | ToothBank |
| Storage of a repository of Teeth, for use in building a HyperGraph. More... | |
| struct | ToothBody |
| Representing bodies of simple tooth inequalities with associated slack. More... | |
| class | TourGraph |
| Wrapper to Concorde CCtsp_lpgraph for pricing cuts at tours. More... | |
| struct | VinfoDeleter |
Typedefs | |
| using | CCsepCall = decltype(&CCtsp_segment_cuts) |
| Alias declaration for Concorde separator call prototype. | |
| using | lpcut_in = CCtsp_lpcut_in |
| using | ToothList = CandidateTeeth::ToothList |
| using | IteratorMat = CandidateTeeth::IteratorMat |
Functions | |
| std::ostream & | operator<< (std::ostream &os, HyperGraph::Type t) |
| std::ostream & | operator<< (std::ostream &os, MetaCuts::Type t) |
| LP::SparseRow | get_row (const CCtsp_lpcut_in &cc_cut, const std::vector< int > &perm, const Graph::CoreGraph &core_graph) |
| SparseRow corresponding to Concorde cut. | |
| LP::SparseRow | get_row (const dominoparity &dp_cut, const std::vector< int > &tour_nodes, const Graph::CoreGraph &core_graph) |
| SparseRow corresponding to simple DP inequality. | |
| LP::SparseRow | get_row (const std::vector< int > &handle_delta, const std::vector< std::vector< int >> &tooth_edges, const Graph::CoreGraph &core_graph) |
| SparseRow corresponding to the handle and tooth edges of a blossom. | |
| template<typename number_type > | |
| double | get_activity (const std::vector< number_type > &x, const LP::SparseRow &R) |
| Function template for determining the activity or lhs of a vector on a row. | |
| std::vector< int > | teeth_inds (const ex_blossom &B, const std::vector< double > &tour_edges, const std::vector< double > &lp_vec, const std::vector< Graph::Edge > &edges, int ncount) |
Gets the indices of the teeth for an ex_blossom B relative to edges. | |
| std::vector< int > | teeth_inds (const ex_blossom &B, const std::vector< double > &tour_edges, const std::vector< double > &lp_vec, const std::vector< Graph::Edge > &edges, int ncount, const std::vector< int > &handle_delta) |
| Like the other version, but if we already have handle_delta. | |
| bool | bad_blossom (const ex_blossom &B, const std::vector< double > &tour_edges, const std::vector< double > &lp_vec, const std::vector< Graph::Edge > &edges, int ncount) |
| Returns true if the blossom is invalid for some reason. | |
| SparseRow | get_row (const dominoparity &dp_cut, const vector< int > &tour_nodes, const Graph::CoreGraph &core_graph) |
| SparseRow | get_row (const vector< int > &handle_delta, const vector< vector< int >> &tooth_edges, const Graph::CoreGraph &core_graph) |
| vector< int > | teeth_inds (const ex_blossom &B, const vector< double > &tour_edges, const vector< double > &lp_vec, const vector< Graph::Edge > &edges, int ncount, const vector< int > &handle_delta) |
| vector< int > | teeth_inds (const ex_blossom &B, const vector< double > &tour_edges, const vector< double > &lp_vec, const vector< Graph::Edge > &edges, int ncount) |
| As above, but without precomputed handle_. | |
| bool | bad_blossom (const ex_blossom &B, const vector< double > &tour_edges, const vector< double > &lp_vec, const vector< Graph::Edge > &edges, int ncount) |
| Same arguments as teeth_inds. More... | |
Variables | |
String names for ConcordeSeparator template instantiation. | |
These need to be defined to pass a string literal as a template parameter, see eg http://www.comeaucomputing.com/techtalk/templates/#stringliteral | |
| constexpr char | seg_fname [] = "CCtsp_segment_cuts" |
| constexpr char | con_fname [] = "CCtsp_connect_cuts" |
| constexpr char | ex_fname [] = "CCtsp_exact_subtours" |
| constexpr char | f2m_fname [] = "CCtsp_fastblossom" |
| constexpr char | gh2m_fname [] = "CCtsp_ghfastblossom" |
| constexpr char | blk_fname [] = "CCtsp_block_combs" |
ConcordeSeparator explicit instantiations. | |
Except for SegmentCuts, all of these are standard heuristics. | |
| using | SegmentCuts = ConcordeSeparator< CCtsp_segment_cuts, false, seg_fname > |
| Exact primal SEC separation. | |
| using | ConnectCuts = ConcordeSeparator< CCtsp_connect_cuts, false, con_fname > |
| Standard connected component SEC generation. | |
| using | ExactSub = ConcordeSeparator< CCtsp_exact_subtours, false, ex_fname > |
| Exact standard SEC separation. | |
| using | FastBlossoms = ConcordeSeparator< CCtsp_fastblossom, true, f2m_fname > |
| Odd component fast blossoms. | |
| using | GHblossoms = ConcordeSeparator< CCtsp_ghfastblossom, true, gh2m_fname > |
| Gr"otschel-Holland blossom heuristic. | |
| using | BlockCombs = ConcordeSeparator< BlkCombCall, true, blk_fname > |
| Block comb separation. | |
| int | BlkCombCall (CCtsp_lpcut_in **c, int *cutcount, int ncount, int ecount, int *elist, double *ecap) |
| Wrapper function because CCtsp_block_combs takes a silent parameter. More... | |
Classes and functions related to cut separation.
Matters related to cuts and separation of cutting planes.
| bool CMR::Sep::bad_blossom | ( | const ex_blossom & | B, |
| const vector< double > & | tour_edges, | ||
| const vector< double > & | lp_vec, | ||
| const vector< Graph::Edge > & | edges, | ||
| int | ncount | ||
| ) |
Same arguments as teeth_inds.
Returns true if B.handle is too small or too big, if there are an even number of teeth returned by teeth_inds, or if the teeth intersect.
|
inline |
Wrapper function because CCtsp_block_combs takes a silent parameter.
| vector<int> CMR::Sep::teeth_inds | ( | const ex_blossom & | B, |
| const vector< double > & | tour_edges, | ||
| const vector< double > & | lp_vec, | ||
| const vector< Graph::Edge > & | edges, | ||
| int | ncount, | ||
| const vector< int > & | handle_delta | ||
| ) |
| [in] | B | the blossom to expand. |
| [in] | tour_edges | the active tour vector. |
| [in] | lp_vec | the lp solution used to find B. |
| [in] | edges | the CoreGraph edges. |
| [in] | ncount | the number of nodes. |
| [in] | handle_delta | the delta_inds for B.handle. Let 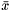 be the edge vector of be the edge vector of tour_edges, 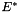 the edges for which the edges for which lp_vec is nonzero, and 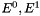 be the edges in be the edges in 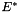 for which for which 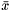 is respectively zero or one. Let is respectively zero or one. Let 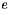 be be B.cut_ind and 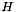 be be B.handle. As per Letchford and Lodi (Primal Separation Algorithms), this function returns
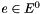 , and , and
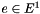 . . |
 1.8.11
1.8.11